The Gauss-Jordan method is used to analyze different systems of linear simultaneous equations that arise in engineering and science. This method finds its application in examining a network under sinusoidal steady state, output of a chemical plant, electronic circuits consisting invariant elements, and more.
The C program for Gauss-Jordan method is focused on reducing the system of equations to a diagonal matrix form by row operations such that the solution is obtained directly. Further, it reduces the time and effort invested in back-substitution for finding the unknowns, but requires a little more calculation. (see example)
The Gauss-Jordan method is simply a modification of the Gauss elimination method. The eliminations of the unknowns is performed not only in the equations below, but in those above as well. That is to say – unlike the elimination method, where the unknowns are eliminated from pivotal equation only, this method eliminates the unknown from all the equations.
The program of Gauss-Jordan Method in C presented here diagonalizes the given matrix by simple row operations. The additional calculations can be a bit tedious, but this method, overall, can be effectively used for small systems of linear simultaneous equations.
In the Gauss-Jordan C program, the given matrix is diagonalized using the following step-wise procedure.
- The element in the first column and the first row is reduced 1, and then the remaining elements in the first column are made 0 (zero).
- The element in the second column and the second row is made 1, and then the other elements in the second column are reduced to 0 (zero).
- Similarly, steps 1 and 2 are repeated for the next 3rd, 4th and following columns and rows.
- The overall diagonalization procedure is done in a sequential manner, performing only row operations.
Source Code for Gauss-Jordan Method in C:
#include<stdio.h>
int main()
{
int i,j,k,n;
float A[20][20],c,x[10];
printf("\nEnter the size of matrix: ");
scanf("%d",&n);
printf("\nEnter the elements of augmented matrix row-wise:\n");
for(i=1; i<=n; i++)
{
for(j=1; j<=(n+1); j++)
{
printf(" A[%d][%d]:", i,j);
scanf("%f",&A[i][j]);
}
}
/* Now finding the elements of diagonal matrix */
for(j=1; j<=n; j++)
{
for(i=1; i<=n; i++)
{
if(i!=j)
{
c=A[i][j]/A[j][j];
for(k=1; k<=n+1; k++)
{
A[i][k]=A[i][k]-c*A[j][k];
}
}
}
}
printf("\nThe solution is:\n");
for(i=1; i<=n; i++)
{
x[i]=A[i][n+1]/A[i][i];
printf("\n x%d=%f\n",i,x[i]);
}
return(0);
}
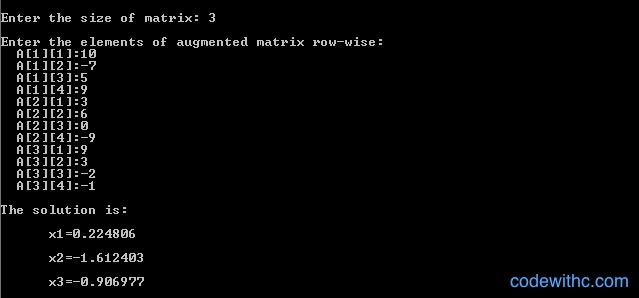
Input/Output:
Note: Let us consider a system of 10 linear simultaneous equations. Solving this by Gauss-Jordan method requires a total of 500 multiplication, where that required in the Gauss elimination method is only 333.
Therefore, the Gauss-Jordan method is easier and simpler, but requires 50% more labor in terms of operations than the Gauss elimination method. And hence, for larger systems of such linear simultaneous equations, the Gauss elimination method is the more preferred one. Find more information about the two methods here.
Also see,
Gauss Jordan Matlab Program
Gauss-Jordan Algorithm/Flowchart
Numerical Methods Tutorial Compilation
The source code for Gauss Jordan method in C language short and simple to understand. This code is to be compiled in Code::Blocks IDE. If you any queries or doubts regarding Gauss-Jordan Method – how it works and what algorithm it follows, discuss them in the comments section.








U have good logic made here. I tried it for 2days but can’t did. Thank u .I understand your code.
I think this is not the Gauss-Jordan Method. The result of Gauss-Jordan Method is a matrix with only 1 in its diagonal and the rest of the elements beside the last column is 0. For example:
1 0 0 2
0 1 0 3
0 0 1 4
Hi please could you explain what exactly the statement if(i!=j){} does in the code I thought the pivot position is when i==j. a reply will be appreciated thanks
Hi, If i want to solve for an array with difference sizes; A[n][n+1]. How will the code be different if that’s the case?
I posted this question on stack overflow, maybe you can give me some advice too?
http://stackoverflow.com/questions/28126232/gauss-jordan-method-in-basic-c-multi?noredirect=1#comment44626215_28126232
This is the Jordan method.
What do you mean by “The Jordan Method”?
Correct me if I am wrong here… but to my understanding the jordan method ignores the elements of the diagonal matrix (during the iterations) while the gauss-jordan method makes the diagonal elements turn to 1.
I tried put zero in some matrix therms e didn’t work! How to fix this problem?
Nice code! I need to do this code using dinamic allocation. Can you help me?